Math 1B  Homework Problem 5.4#18

 

This problem belongs to a larger class of problems:  Find the interval on which the function  is concave upward.  Assume that a and k are both positive.

 

Solution:

 

 

 

An example of this is 5.4#18: .  While it’s not essential to the problem, it’s nice to find an antiderivative using trig substitution.  Note the sum of squares (well, 3 is the square of its square root)  so we’d like to have , which we can obtain by substituting , or, more simply,  whence  and the integral becomes  

This is just a transformation of the arctan function that, among other things, shifts its inflection point from the origin to the point .  On the TI-89 (or Voyage 200) we can plot the function by first defining it like so:

The plot comes out all right, but only after an eternity of waiting:

Alternatively, you can do the integral:

which gives the same plot, only much faster:

 

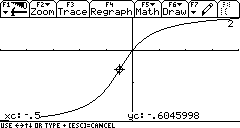
Note that the integral function goes through the origin.  Do you see why that makes sense?